Camera calibration
研究现有相机标定的方法的步骤和机理,探讨主动视觉的标定新方法,张正友法,相机纯旋转运动,相机平移运动的对极几何约束,三角测量方法,变焦距成像模型;
张正友法机理
1)标定模型的建立
2)单映性矩阵H的求解
将H矩阵变换成向量的形式:
带入成像模型得到下式子,含有 8 个未知数,因此只需要获取到 4 个及以上的图像的空间参考点世界坐标,便可以利用最小二乘法求解得到 h ,进而恢复单映性矩阵 H;
3)内参数的求解
因为R为正交矩阵:
可得到下列关系:
B 为一个对称矩阵:
将B矩阵变成向量形式,然后可得到如下关系:
其中:
Extraction of the Intrinsic Parameters from Matrix B:$B = λK^{−T}K$
4)内外参数的优化求解
以上步骤得到的相机参数是从数值意义上得到的(即为数值解),并不具有物理意义。因此,Zhang 的方法接下来利用最大似然估计的方法,从物理意义上进一步优化求解以上参数。 对于拍摄的n幅图像(每幅图像上选择 m 个特征点),建立以空间特征点实际投影和理想投影误差最小为目标的代价函数:
通过将步骤 3)中计算得到的结果作为初值,带上式 ,利用 Levenberg-Marquardt 迭代 算法优化求解得到最终的相机内外参数。
通常情况下,相机的镜头是包含畸变的。因此,在综合考虑畸变和噪声的影响后:
加入相机二维纯旋转运动(俯仰运动和偏航运动)约束后:
$H$为相机内参数,$[R_{1},T_{1}]$为初始相机外参数,$s$为尺度因子,$R_{Ti}$为第$i$幅图像与初始图像的旋转矩阵,可以通过经纬仪得到;
非线性优化:Levenberg-Marquardt algorithm
初始值:像素尺寸dx和dy、焦距f、分辨率W*H;外参初始矩阵可以通过P3P算法求解得到;
优化函数:
$(R_{ct},T_{ct})$为相机和经纬仪的变换参数,在实际装配过程中应尽量保证相机坐标系与经纬仪坐标系重合,使得$R_{ct}$的初始值为单位矩阵,$T_{ct}$的初始值为$[0,0,0]^{T}$
加入相机纯平移运动约束后:
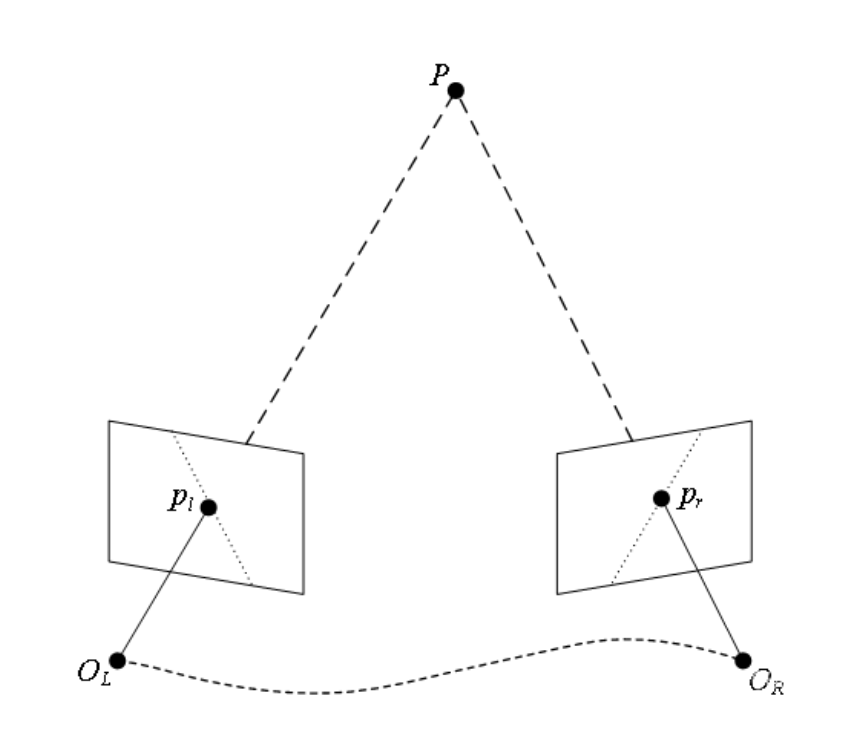
如图1所示,以其中一对匹配点为例。$P$为空间中的一点(坐标未知),其在左边图像中的投影为$P_l = [u_l,v_l,1 ] ^T$,在右边图像中的投影为$P_r = [u_r,v_r,1 ] ^T$,当我们以相机坐标系$O_L$为参考坐标系时,有:
其中${s}_l、{s}_r$分别为点$P$在相机坐标系$O_L$、$O_L$中的$ z $坐标值(即深度),$K $为3 X 3的相机内参矩阵,$R 、t $即为$O_L$、$O_L$之间的相对位姿关系。取$x_l = K^{-1} P_l$,$x_r = K^{-1} P_r$, 则有:
上式两边同时左乘$t$的反对称矩阵$t^{\wedge}$,相当于两侧同时与t做外积($t$ 与自身的外积$t^{\wedge} t = 0$):
然后,两侧同时左乘$x^{T}_{r}$ :
上式左侧中,$ t $ 与 $ x_{r}$ 的外积$t^{\wedge} x_{r}$ 是一个与$ t $ 和 $ x_{r} $都垂直的向量,所以,再将$x^{T}_{r}$ 与 $t^{\wedge} x_{r}$做内积,其结果必为0,从而有:
(5)式以非常简洁的形式描述了两幅图像中匹配点对$ p_l$和$ p_r$之间存在的数学关系,这种关系就叫对极约束。另外,我们称$E = t^\wedge R$ 为本质矩阵(Essential Matrix),称$ F = K^{-T} t^\wedge R K^{-1} = K^{-T} E K^{-1}$为基础矩阵(Fundamental Matrix)),于是(5)式可以进一步简化为:
现在我们需要重新明确一下对极几何的工作:对极几何是要利用已知的$n$对如上述$p_l$、$ p_r$这样的匹配点(二维像素坐标),来计算相机的运动$R$, $t$,即求解本质矩阵 $ E $ 或基础矩阵 $F $。
对极几何存在的问题:根据对极约束求解得到的相机旋转运动R RR是准确的,平移运动t tt是不具备真实尺度的。
三角测量原理:
三角测量(Triangulation)又叫三角化,是根据前后两帧图像中匹配到的特征点像素坐标以及两帧之间的相机运动$R$、$t$,计算特征点三维空间坐标的一种算法。直观来讲,当有两个相对位置已知的相机同时拍摄到同一物体时,如何根据两幅图像中的信息估计出物体的实际位姿,即通过三角化获得二维图像上对应点的三维结构,这正是三角测量要解决的问题。
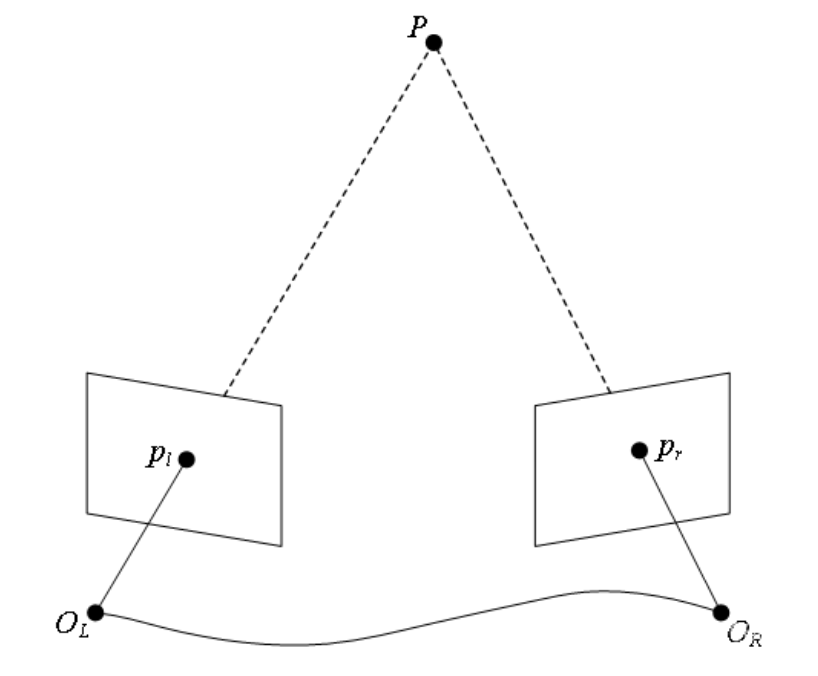
如图所示为三角测量基本原理的示意图,该图与相机平移运动对极几何关系图非常相似,但应该注意其中的区别:此时我们已经知道了$O_L$与$O_R$的关系,$p_l$、$p_r$也是已知的,要求的是$P$的三维空间坐标。由(1)式我们知道,要求点$P$的三维坐标,需要先求深度$ s$ ;由(2)式我们有:
对上式两侧左乘一个$x_r$的反对称矩阵$x_r^\wedge$,得:
(8)式是一个超定方程组(Overdetermined system),通常只能求得它的最小二乘解。当我们求出$s_l$后,根据(7)式就很容易求出$s_r$,最后由(1)式,我们有:
上式中$P_{O_L}$与$P_{O_R}$之间的关系为:
即:以$O_L$标系为参考,$O_R$经过运动$R$ 、$t$变换到$O_L$,那么原来在$O_L$坐标系下的点$P$在$O_R$坐标系下表示为$P_{O_R}=RP_{O_L}+t$。如果我们还知道相机与世界坐标系的变换关系$T$,就可以将$P_{O_L}$或$P_{O_R}$转换到世界坐标系下表示,得到点$P$的世界坐标。
同一特征点点变焦距成像模型:
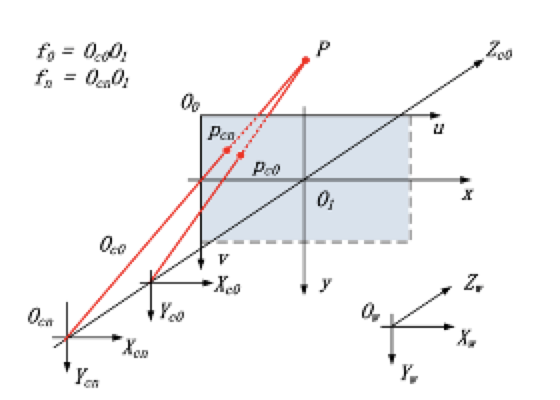
该模型包括 5 个坐标系:世界坐标系$O_wX_wY_wZ_w$ 、变焦相机基坐标系${O}_{c0}X_{c0}Y_{c0}Z_{c0}$ 、变焦相机动坐标系${O}_{cn}X_{cn}Y_{cn}Z_{cn}$、图像物理坐标$O_{1xy}$、图像像素坐标系$O_{0uv}$;
当变焦相机的焦距位于任意位置$f_n$时,物体的三维空间点P通过变焦相机的动坐标系光心$O_{cn}$,并映射到变焦相机的像平面上点$p_{cn}$位置。当变焦相机的焦距位于$f_0$时,点P通过变焦相机的基坐标系光心$O_{c0}$,并映射到变焦相机的像平面上点$p_{c0}$位置。
变焦相机动坐标系${O}_{cn}X_{cn}Y_{cn}Z_{cn}$的$Z_c$轴与相机的光轴 $Z_{c0}$重合,它垂直于图像平面并通过图像坐标系的中心,$X_{cn}$轴和$Y_{cn}$轴分别平行于图像坐标系的u轴和v轴,光心到图像平面的距离 $O_{cn}O_1$称为变焦相机的实时焦距$f_n$,设变焦相机坐标系${O}_{cn}X_{cn}Y_{cn}Z_{cn}$中的物体空间点 P 在图像物理坐标系$O_{1xy}$下的成像像点为$p_{cn}=[x,y]T$ ,则可以得到:
根据相机坐标系下空间点和图像点之间的转换关系,相机的内参数矩阵由式中矩阵 M1 表示。当空间变焦相机的焦距位于基准焦距 f0 时,可以得到:
当相机的焦距发生改变,$\alpha_{x}=\frac{f_{c n}}{d x}$为u轴上的放大系数,$\alpha_{y}=\frac{f_{c n}}{d y}$为v轴上的放大系数,相机的外参数矩阵用$M_2$表示,$T_{wen}$为3×1平移矩阵,$R_{wen}$为3×3为正交旋转矩阵,则三维空间点与二维图像点之间的映射关系可以通过下式进行描述:
标定存在的一些问题:
the assumption of pure rotation is often violated because the optic centre of the camera and the rotation centre do not completely coincide.