Vincenty solutions of geodesics on the ellipsoid

Distances and bearings between points on an ellipsoidal-model earth

Vincenty’s solution for the distance between points on an ellipsoidal earth model is accurate to within 0.5 mm distance

We can use live examples at https://www.movable-type.co.uk/scripts/latlong-vincenty.html

You can git the Matlab Version at git@github.com:Jason-Yoo/Vincenty-solutions.git

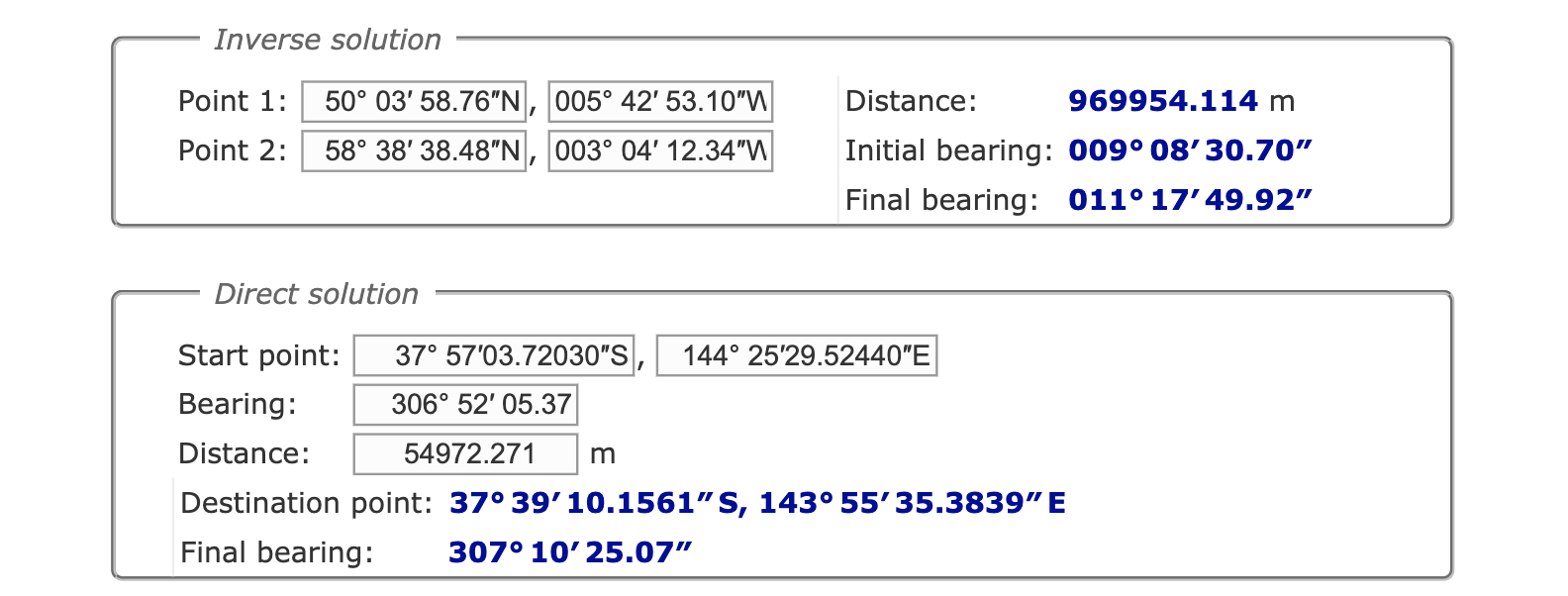
  首先将起点P1和终点P2的纬度转换为弧度记为φ1，φ2，并计算经度差：

$$\Delta L=(\pi / 180)\left(L_{2}-L_{1}\right)$$

  对P1、P2点点纬度进行归化处理:

$$\begin{array}{l}U_{1}=\arctan \left[(1-f) \tan \phi_{1}\right] \\ U_{2}=\arctan \left[(1-f) \tan \phi_{2}\right]\end{array}$$

  设初始条件$ \lambda_0 = \Delta L$，迭代公式：

$$\begin{aligned} \lambda_{k+1}=& \Delta L+(1-C) f \sin \alpha\{\sigma+C \sin \sigma X\\ &\left.\left[\cos 2 \sigma_{m}+C \cos \sigma\left(-1+2 \cos ^{2} 2 \sigma_{m}\right)\right]\right\} \end{aligned}$$

  当$\varepsilon = 10^{-12}$,迭代终止：

$$\left|\lambda_{\mathrm{k}+1}-\lambda_{\mathrm{k}}\right|<\varepsilon$$

  式中 $\alpha$ 为大椭圆航线在赤道的方位角；$\sigma$ 为起点与终点间的球面角距；$\sigma_m$ 为大椭圆航线与赤道的交点到大椭圆航线中点点球面角距。

  最后分别计算距离$s$、起点和终点各自的方位角度𝜶1、𝜶2，𝜶1是起点经线按顺时针方向到大椭圆航线夹角，𝜶2是终点经线按顺时针方向到大椭圆航线夹脚；

$$u^{2}=\cos ^{2} \alpha \cdot\left(a^{2}-b^{2}\right) / b^{2}$$ $$\begin{aligned} A=& 1+\frac{u^{2}}{16384}\left\{4096+u^{2} \cdot\left[-768+u^{2}\left(320-175 u^{2}\right)\right]\right\} \end{aligned}$$ $$B=u^{2} / 1024 \cdot\left\{256+u^{2} \cdot\left[-128+u^{2} \cdot\left(74-47 \cdot u^{2}\right)\right]\right\}$$ $$\begin{aligned} \Delta \sigma &=B \cdot \sin \sigma \cdot\left\{\cos 2 \sigma_{\mathrm{m}}+B / 4 \cdot\left[\cos \sigma \cdot\left(-1+2 \cdot \cos ^{2} 2 \sigma_{\mathrm{m}}\right)\right.\right.\\-&\left.\left.B / 6 \cdot \cos 2 \sigma_{\mathrm{m}} \cdot\left(-3+4 \cdot \sin ^{2} \sigma\right) \cdot\left(-3+4 \cdot \cos ^{2} 2 \sigma_{\mathrm{m}}\right)\right]\right\} \end{aligned}$$ $$s=b A(\sigma-\Delta \sigma)$$ $$\alpha_{1}=\operatorname{atan}\left(\cos U_{2} \cdot \sin \lambda / \cos U_{1} \cdot \sin U_{2}-\sin U_{1} \cdot \cos U_{2} \cdot \cos \lambda\right)$$ $$\alpha_{2}=\operatorname{atan}\left(\cos U_{1} \cdot \sin \lambda /-\sin U_{1} \cdot \cos U_{2}+\cos U_{1} \cdot \sin U_{2} \cdot \cos \lambda\right)$$

  式中：$a=6378137.0m,b≈6 356752.314245m$ 分别为WGS-84椭球的长半轴和短半轴。