Camera Pose and Focal Length Estimation

1.未知焦距位姿测量—PNP问题

关键词：Focal Length Estimation 、 Camera Pose Estimation、 PNP Problem

方法一：通过成像模型和相机模型，对相机内参数矩阵利用点之间的距离关系等构件多项式代数方程，通过隐变量消去法或Grobner基，吴方法的方式进行求解；

位姿估计的最小问题：

​ 所谓最小问题,是指使用最少的匹配点对来估计对极几何、相机标定参数以及畸变参数等，但是最小问题的求解一般需进行复杂的代数多项式求解，最初的算法都选择忽略几何限制直接使用更多的点对进行求解。随着 Grobner 基的应用， 复杂多项式方程组的求解变得可行，推动了基于最小问题相对姿态估计的快速发展。

Major contributors：Zuzana Kukelova

相关文献：

[1]. Kanaeva, Ekaterina, Gurevich, Lev, Vakhitov, Alexander. Camera Pose and Focal Length Estimation Using Regularized Distance Constraints[C]// British Machine Vision Conference. 2015.

​ 基于正则距离约束进行相机姿态和焦距估计，文章开头阐述了基于EPNP的位姿计算方法，然后在这个基础上提出了基于正则距离约束的位姿计算方程，将投影方程和距离约束合并为一个具有统计意义的最小二乘函数，将搜索空间定义为最小二乘系统矩阵的几个右奇异向量的线性组合，然后使用线性规划技术求出最优解；

​ 实验表明，其提出的方法EPNPfr,在提取误差存在3～4个像素误差时，其位姿估计误差和焦距估计误差均在10%左右，在点数超过10个以后，其位姿估计误差和焦距估计误差均在4%以下，当点数达到15个及以上，其误差在2%左右；

[2].薛俊诗, 舒奇泉, 郭宁博. 未知畸变参数时多视图三维重建相对位姿估计方法[J]. 光子学报, 2018

​ 根据对极几何关系，推导了畸变中心未知时的畸变基础矩阵表达模型． 在系数矩阵中引入加权矩阵，控制参与估计的匹配对应点，通过奇异值分解估计畸变基础矩阵．根据加权矩阵更新准则对加权矩阵进行更新，然后进行迭代计算，比较前后两次估计得到的内点数目及平均极线距离，得到畸变基础矩阵的最优解，并判断是否需要继续迭代． 在得到最优畸变基础矩阵后，再分别对畸变中心、畸变参数以及焦距进行估计．

​ 算法误差：在噪声均方差为2.5时，畸变参数误差均值小于 2%，3.5% ．

[3].Kukelova, Zuzana , et al. “Fast and robust numerical solutions to minimal problems for cameras with radial distortion.” Computer Vision & Image Understanding 114.2(2010):234-244.

​ 提出了一种基于八个对应点的最小解决方案 可以估计未标定相机的基础矩阵以及单一畸变参数。

[4].Jiang, Fangyuan, Kuang, Yubin, Solem, Jan Erik. A Minimal Solution to Relative Pose with Unknown Focal Length and Radial Distortion.[M]// Computer Vision — ACCV 2014. Springer International Publishing, 2014.

​ 对未知焦距及畸变参数下的本质矩阵估计的最小问题进行了详细的研究, 提出了基于 Grobner 基的多项式求解方法 ， 该方法能够得到大量正确的匹配对应点并实现焦距及 畸变参数的同时精确估计 。

[5]. KUKELOVA Z，HELLEＲ J，BUNJNAK M，et al． Efficient solution to the epipolar geometry for radially distorted cameras[C］. IEEE International Conference on Computer Vision，2015

​ 通过 10 个点对构建了自由度为 10 的多项式方程，并利用 Strum 序列法进行求解，能够得到抗噪声、稳定的、快速的求解，除本质矩阵与基础矩阵外，单应矩阵也是描述对极几何关系的重要内容 。

[6]. KUKELOVA Z，HELLEＲ J，BUJNAK M，et al． Ｒadial distortion homography［C］．Computer Vision and Pattern Recognition， IEEE，2015： 639-647．

​ 研究了畸变情况下单应矩阵的最小求解方法（使用五个对应点构建非线性方程组，并使用 Grobner 基进行快速稳定求解）和非最小求解方法（是使用六个点构建二元二次线性方程组，进行线性求解 ），上述畸变参数的求解都是建立在已知畸变中心（Center of Distortion，CoD），或者假定畸变中心为影像中心下进行的。实际上，影像的畸变中心与影像中心并不重合 ．

2.未知焦距测量—标定测量问题

关键词：相机自标定 成像模型 相机内参数

方式一：当目标运动轨迹任意时，从像平面轨迹中恢复轨迹的空间信息，须要获取相机的位姿．从图像中标定相机位姿的方法主要有：

a. 模板标定法，主要有Tsai 标定法与张正友标定法；

b. 主动标定法， 如基于椭圆特征的平面位姿定位方法和基于测量辅助工具法，但是主动标定实验条件要求高，受标定物的影响较大；

c. 自标定法，如在使用扫描曲线标定 CT、基于镜像与正交性约束、基于透视图中的灭点和利用地标测量的平面运动约束估计相机的位姿信息．但是以上的标定法均使用静态图片进行相机标定，不适用于轨迹分析中的目标特征运动变化的具体情况

方式二：通过建立的合作目标对变焦相机不同倍率和焦距设置下的变焦相机模型进行标定，获得不同倍率和焦距设置下的标定参数，然后通过这系列位置的标定模型参数进行分析，建立变焦相机的几何模型。

相关文献:

[1] . 变焦相机高精度标定与测图精度研究 2015 杨长坤

将变焦相机分解成多个定焦相机，建立包含缩放倍数和焦距变化的变焦相机模型，通过建立的合作目标对变焦相机不同倍率和焦距设置下的变焦相机模型进行标定，获得不同倍率和焦距设置下的标定参数，然后通过这系列位置的标定模型参数进行分析，建立变焦相机的几何模型。

具体方法：

（1）.首先基于合作特征分别对变焦相机固定主距位置进行标定；

（2）.对不同率和焦距设置下的标定结果进行多项式拟合得到变焦相机几何模型；

结论：标定出的主点随意的分布，这种随意性在倍率及焦距变化时都有表现，因此很难通过多项式拟合的方式标定像主点，但是也可以看出这种变化性不大，不同倍率和焦距之下主点的差异不超过10个像素，因此可借助吴波提出的焦距扩展的方法标定像主点，由此得到在焦距和倍率变化时的主点标准差为0.001mm

[2]. 段绍丽. 变焦相机的标定技术研究[D].2017.郑州大学

研究了基于二消式自标定方法。提出的基于二消失点的相机自标定方法，只需被拍摄场景中包含矩形图案（需要满足建立二消失点的条件，两组正交平行的线），从不同视点拍摄4幅图像，利用亚像素角点检测算法计算二消失点，根据二消失点的几何性质建立线性约束方程，最后线性求解出相机的内参数；

标定精度：焦距标定误差2%，主点标定误差3%，适合近距离标定；

缺点：需要两个视角的4幅图像，且被拍摄场景中包含矩形图案；

[3]. 顾国华.二维旋转平台下的相机参数标定.2017. 南京理工大学

提出了一种基于二维旋转平台的相机成像模型。 首先，通过一对坐标系的变换与逆变换，将相机的旋转平移变换关系转换为二维旋转平台纯旋转关系；然后，借助旋转平台读数以及相机到旋转平台的固定变换关系，实现相机内参的精确标定以及任意位置间相机外参的相互转换；最后，利用标定出的相机与旋转平台间变换矩阵实现不同位置相机参数的转换。

求解模型：

$H$为相机内参数,$[R_{1},T_{1}]$为初始相机外参数，$s$为尺度因子，$R_{Ti}$为第$i$幅图像与初始图像的旋转矩阵，可以通过经纬仪得到

$$\begin{aligned}\left[\begin{array}{c}s_{i} \boldsymbol{p}_{i} \\ s_{i} \\ 1\end{array}\right]=\left[\begin{array}{cc}\boldsymbol{H} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{1}\end{array}\right] \times\left[\begin{array}{cc}\boldsymbol{R}_{\mathrm{ct}} & \boldsymbol{T}_{\mathrm{ct}} \\ \boldsymbol{0} & \boldsymbol{1}\end{array}\right]^{-1} \times\left[\begin{array}{cc}\boldsymbol{R}_{T i} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{1}\end{array}\right] \times \left[\begin{array}{cc}\boldsymbol{R}_{\mathrm{ct}} & \boldsymbol{T}_{\mathrm{ct}} \\ \mathbf{0} & \mathbf{1}\end{array}\right] \times\left[\begin{array}{cc}\boldsymbol{R}_{1} & \boldsymbol{T}_{1} \\ \mathbf{0} & \mathbf{1}\end{array}\right] \times \boldsymbol{P} \end{aligned}$$

非线性优化：Levenberg-Marquardt algorithm

初始值：像素尺寸dx和dy、焦距f、分辨率W*H；外参初始矩阵可以通过P3P算法求解得到；

$$\boldsymbol{H}=\left[\begin{array}{ccc}\frac{f}{d x} & 0 & \frac{W}{2} \\ 0 & \frac{f}{d y} & \frac{H}{2} \\ 0 & 0 & 1\end{array}\right]$$

优化函数：

$(R_{ct},T_{ct})$为相机和经纬仪的变换参数，在实际装配过程中应尽量保证相机坐标系与经纬仪坐标系重合，使得$R_{ct}$的初始值为单位矩阵，$T_{ct}$的初始值为$[0,0,0]^{T}$

$$\begin{array}{c}f\left(\boldsymbol{H}, \boldsymbol{R}_{\mathrm{ct}}, \boldsymbol{T}_{\mathrm{ct}}, \boldsymbol{R}_{1}, \boldsymbol{T}_{1}\right)_{\min }= \ \sum_{i=1}^{N}\left\|\boldsymbol{p}_{i}\left(\boldsymbol{H}, \boldsymbol{R}_{\mathrm{ct}}, \boldsymbol{T}_{\mathrm{ct}}, \boldsymbol{R}_{1}, \boldsymbol{T}_{1}\right)-\boldsymbol{p}_{i}^{\prime}\right\|\end{array}$$

[4]. 雷成, 吴福朝, 胡占义. 一种新的基于主动视觉系统的摄像机自标定方法[J]. 计算机学报, 2000(11):11-20.

提出了一种新的基于主动视觉系统的摄像机自标定方法 ,通过控制摄像机平台作 4次平移运动 (其中任意 3次均不在同一平面上 )即可线性地标定摄像机的内参数以及摄像机坐标系与平台坐标系之间的旋转矩阵 .

首先通过主动视觉平台纯平移运动对内参数阵 K以及摄像机坐标系与平台 坐标系之间的旋转矩阵 Rp 的标定，然后，通过平台平移和旋转运动对摄像机坐标系与平台坐标系之间的平移向量 Tp 的标定

[5].李宝全, 方勇纯, 张雪波. 基于纯旋转运动的摄像机统一自标定方法[J]. 光学学报, 2013(11):146-153.

​ 应用统一球形成像模型对中心折反射摄像机与针孔摄像机两类摄像机进行描述；证明当摄像机坐标系做纯旋转运动时，空间静止点对应的球面投影点之间的距离保持不变；根据该性质构造具有统一形式的内参数约束方程组；提出最优化目标函数（Levenberg-Marquardt algorithm）并利用数值优化算法进行求解。

其中：

$$a=\frac{u-u_{0}}{f_{u}(\xi+m)}, \quad b=\frac{v-v_{0}}{f_{v}(\xi+m)}$$ $$\lambda=\frac{\xi+\sqrt{1+\left(1-\xi^{2}\right)\left(a^{2}+b^{2}\right)}}{a^{2}+b^{2}+1}$$ $$\boldsymbol{K}_{m}=\left[\begin{array}{ccc}f_{u}(\xi+m) & 0 & u_{0} \\ 0 & f_{v}(\xi+m) & v_{0} \\ 0 & 0 & 1\end{array}\right]$$

对于针孔相机模型：$\xi=0,m=1$​

优化模型：

$$\begin{aligned} J\left[\xi, f_{u}(\xi+m), f_{v}(\xi+m), u_{0}, v_{0}\right]=& \sum_{i=1}^{N-1} \sum_{j=i+1}^{N}\left\{\left[a_{i} \lambda_{i} a_{j} \lambda_{j}+b_{i \lambda} b_{j} \lambda_{j}+\left(\lambda_{i}-\xi\right)\left(\lambda_{j}-\xi\right)\right]-\right.\\ &\left.\left[a_{i \lambda}^{\prime} \lambda_{i}^{\prime} a_{j}^{\prime} \lambda_{j}^{\prime}+b_{i}^{\prime} \lambda_{i}^{\prime} b_{j}^{\prime} \lambda_{j}^{\prime}+\left(\lambda_{i}^{\prime}-\xi\right)\left(\lambda_{j}^{\prime}-\xi\right)\right]\right\}^{2} \end{aligned}$$

[6].高扬, 林嘉睿, 陈家琪,等. 基于精密二轴转台的大尺寸测量相机高效灵活标定方法[J]. 纳米技术与精密工程, 2018, 1(001):59-65.

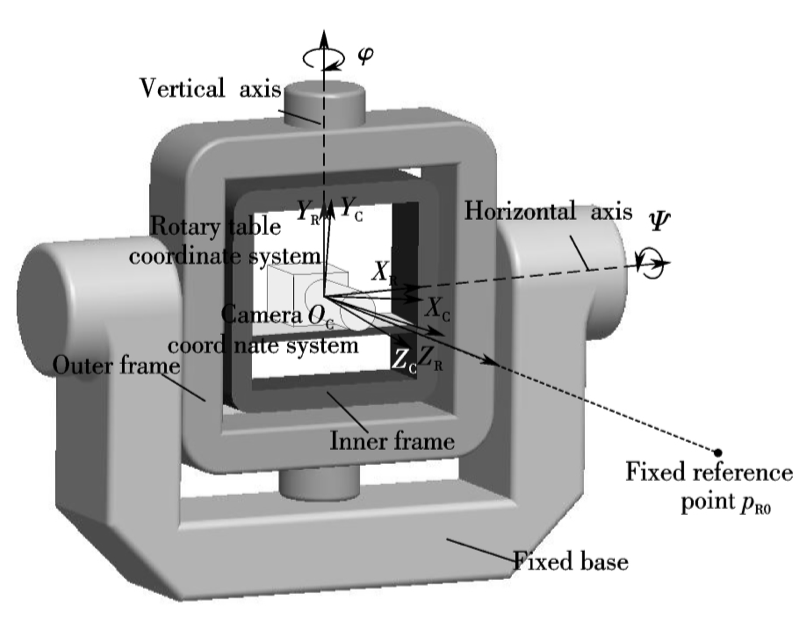
研究了一种使用精密二轴转台和单个固定不动的光学参考点进行相机标定的方法。 通过精密二轴转台带动相机做二维转动并拍摄前方光学参考点，从而构建精密的角度基准控制场并实现标定．

$P_{R0}$为固定不动光点，$R_i$为转台变换量

求解模型：

$$\boldsymbol{R}_{i}=\left[\begin{array}{ccc}\cos \varphi_{i} & 0 & -\sin \varphi_{i} \\ 0 & 1 & 0 \\ \sin \varphi_{i} & 0 & \cos \varphi_{i}\end{array}\right]\left[\begin{array}{ccc}1 & 0 & 0 \\ 0 & \cos \psi_{i} & \sin \psi_{i} \\ 0 & -\sin \psi_{i} & \cos \psi_{i}\end{array}\right]$$ $$\left.\begin{array}{l}z_{C i}\left[\begin{array}{l}u_{i} \\ v_{i} \\ 1\end{array}\right]=\left[\begin{array}{ccc}a_{x} & 0 & u_{0} \\ 0 & a_{y} & v_{0} \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{l}x_{c i} \\ y_{c i} \\ z_{c i}\end{array}\right]= {\left[\begin{array}{ccc}a_{x} & 0 & u_{0} \\ 0 & a_{y} & v_{0} \\ 0 & 0 & 1\end{array}\right]\left[\boldsymbol{R}_{\mathrm{RC}} \boldsymbol{R}_{i}\left[\begin{array}{c}x_{\mathrm{R} 0} \\ y_{\mathrm{R} 0} \\ z_{\mathrm{R} 0}\end{array}\right]+\boldsymbol{t}_{\mathrm{RC}}\right.}\end{array}\right]$$

非线性优化方法：Levenberg-Marquardt algorithm

优化模型：将$P_{R0}$归一化后

$$\begin{aligned} \boldsymbol{J}\left(\boldsymbol{p}_{\mathrm{R} 0}, \boldsymbol{R}_{\mathrm{RC}}, \boldsymbol{x}_{\mathrm{ins}}\right)=& \left[\sum_{i=1}^{n} \left(\hat{u}_{i}-u_{i}\right)^{2}+ \left(\hat{v}_{i}-v_{i}\right)^{2} \right]+M \left(\left\|\boldsymbol{p}_{\mathrm{R} 0}\right\|-1\right)^{2} \end{aligned}$$

[7].霍炬, 杨卫, 杨明. 基于消隐点几何特性的摄像机自标定方法[J]. 光学学报, 2010, 30(002):465-472.

基于正交的两组平行直线形成的消隐点的几何特性，提出了一种摄像机内外参数的自标定方法。 该方法利用连接光心与消隐点向量的正交性质，建立关于相机内参数的约束方程，并给出了约束方程的线性解法；

针对现有自标定方法未能标定畸变系数的现状，提出了一种考虑畸变的非线性最优化算法，该算法以线性求解得到的内参数为初值，利用非线性单纯型法寻优标定畸变；建立消隐点坐标系，给出了摄像机外参数的求解算法。

[8].Agapito, L., Hayman, E., Reid, I.: Self-calibration of rotating and zooming cameras. Int. J. Comput. Vis. 45(2), 107–127 (2001)

提出了新的线性和非线性校准方法（基于LM算法），用于自校准旋转和变焦相机。 他们的方法基于无限单应性约束，并将$f，C_x，C_y$和$k_1$视为变量参数。 为了提高相机参数的准确性，他们使用了最大似然估计（MLE）和最大后验估计（MAP）。 他们通过保持原理点不变而更准确的结果。 他们还分析了径向畸变对自校准的影响，并使用多项式拟合对径向畸变的第一系数的变化进行了建模。