机器人手眼标定Ax=xB(求解相机和机械臂末端坐标系位姿关系)
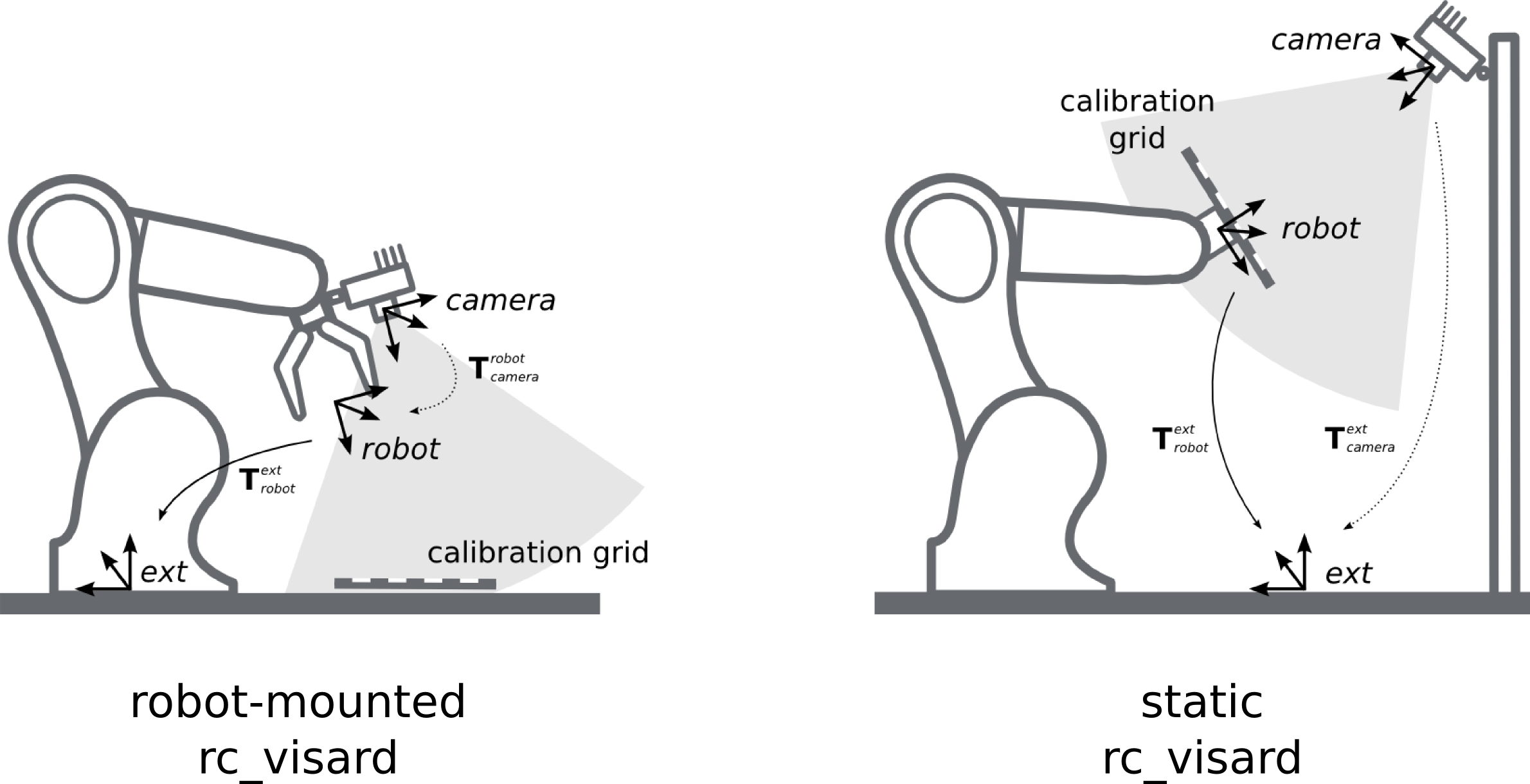
eye in hand(机械臂底座与相机相对位姿固定)
代表从机器人末端(gripper/robot)到机器人基座(end/base)的齐次变换矩阵。
为相机到目标的变换矩阵,
代表了两个末端达到的位置。
根据机器人基座与目标/标定板之间位置相对固定的关系建立以下等式:
常用标定方法:Tsai-Lenz标定
eye to hand(机械臂底座与标定板相对位姿固定)
常用标定方法:
九点标定—直接建立相机和机械臂末端的坐标变换关系
方法:让机械手的末端去走这就9个点得到在机器人坐标系中的坐标,同时还要用相机识别9个点得到像素坐标。这样就得到了9组对应的坐标。
手眼标定具体步骤:
- 进行相机内参标定(张正友标定法);
- 使用eye-to-hand或者eye-in-hand的方式将相机、标定板固定好,启动机器人调整机械臂末端位置姿态,并将对应的照片、机器人末端位姿记录下来;
- 利用相机内参计算得到照片中相机与标定板之间的坐标转换关系;
- 利用“两步法”求解基本方程。先从基本方程中求解R,再求解T,其中特征点世界坐标为A组数据,末端坐标为B组数据;
“两步法”手眼标定
一般用“两步法”求解基本方程,即先从基本方程上式求解出$R_{cg}$,再代入下式求解出$T_{cg}$。在TSAI文献中引入旋转轴-旋转角系统来描述旋转运动来进行求解该方程组,具体的公式推导可以查看原始文献,这里只归纳计算步骤,不明白的地方可阅读文献,计算步骤如下:
Step1:利用罗德里格斯变换将旋转矩阵转换为旋转向量
Step2:向量归一化
Step3:修正的罗德里格斯参数表示姿态变化
Step4:计算初始旋转向量$P_{cg}^{‘}$
Step5:计算旋转向量$P_{cg}$
Step6:计算旋转矩阵$R_{cg}$
Step7:计算平移向量$T_{cg}$
备注:
计算两组数据的变换矩阵实际上为3D-3D的位姿估计问题,可用迭代最近点(Iterative Closest Point, ICP)求解,实现方法有两种:
1.利用线性代数的求解(主要是 SVD)(建议采用该方法)
2.利用非线性优化方式的求解(类似于 Bundle Adjustment)