本质矩阵(Essential Matrix):
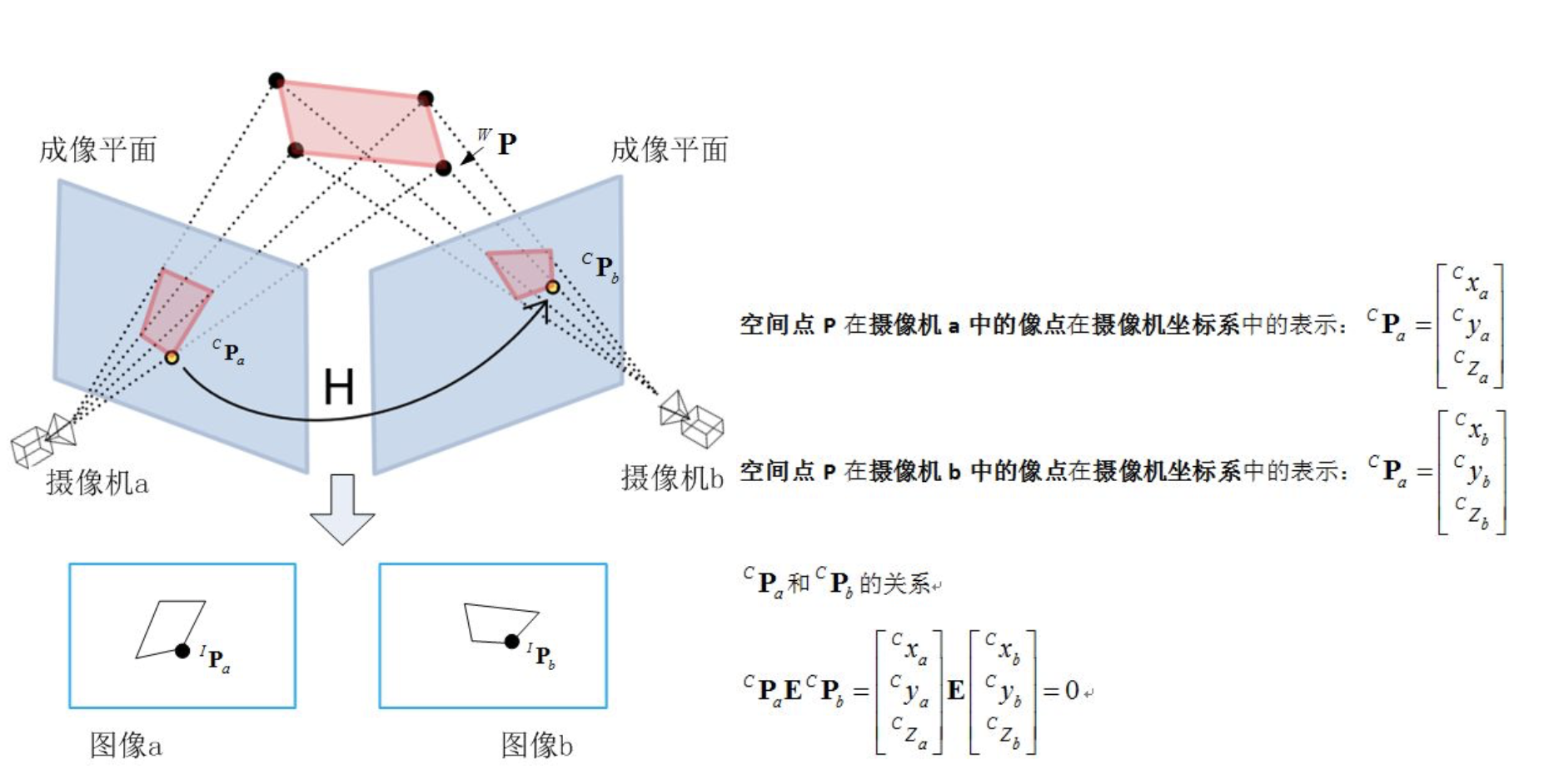
本质矩阵E:反映【空间一点P的像点】在【不同视角摄像机】下【摄像机坐标系】中的表示之间的关系,具有5个自由度。
基础矩阵(Fundmental Matrix):
在对极几何中存在一个从一幅图像上的点到另一幅图像与之对应的极线的映射,基础矩阵即表示该射影映射,基础矩阵具有7个自由度。

单应矩阵(Homography Matrix):
单应性(Homography)变换。可以简单的理解为它用来描述物体在世界坐标系和像素坐标系之间的位置映射关系。对应的变换矩阵称为单应性矩阵,它同时包含了相机内参和外参。射影变换的自由度为9,其同样具有尺度等价性(因为图像坐标是通过齐次坐标表示,因此你矩阵同乘一个常数,最后求得的坐标其实是一致的),因此自由度减一,其自由度为8。
计算机视觉领域广泛应用的畸变模型:
$\begin{equation}
\left[\begin{array}{lll}{x,} & {y,} & {1+k\left(x^{2}+y^{2}\right)}\end{array}\right]^{\top} \simeq P X
\end{equation}$
其中 $(x,y)$ 为投影的3D点 $X$ 的中心图像坐标,其中 P 为摄像机投影矩阵,$k$为畸变系数;
来源:
Simultaneous linear estimation of multiple view geometry and lens distortion
解决的问题:3D-2D点的矫正(由于镜头畸变造成)
解决模型:
1.真正的镜头畸变曲线通常非常复杂,而处理非线性畸变的系统需要使用高阶模型或查找表来校准相机。然而,对于计算机视觉,特别是对于匹配,像素顺序的精度是很重要的。因此,通常将失真函数L扩展为泰勒级数,并且只保留第一个非线性偶数项;
2.新的失真方程